La economía de Interstellar

Imagen: Warner Bros. / Syncopy / Paramount Pictures / Legendary Pictures / Lynda Obst Productions.

Fantástico artículo sobre economía, física cuántica y actualidad. Tiene todo lo que me gusta en divulgación: contenido, información, rigor, ironía, didáctica e interés. 

Publicado por: Enrique F. Borja en JOT DOWN cultural magacine

Supongo que estaréis al tanto de que no hace mucho salió una película, Interstellar, que permitió a los físicos y físicas de todo el mundo ponerse divinos y hablar de cosas tales como agujeros de gusano, agujeros negros, exoplanetas y dilataciones temporales, muchas dilataciones temporales.

Se ha discutido hasta la saciedad sobre el fundamento científico de la película, unas veces con más fortuna que otras, pero aquí lo importante es participar. Sin embargo, me parece imperdonable la falta de visión que hemos mostrado todos al no percatarnos de que la película nos plantea un problema jodido donde los haya. No, no tiene nada que ver con la plausibilidad de la existencia de agujeros de gusano en un universo de cinco dimensiones. Tampoco sobre lo increíble de seres posthumanos pentadimensionales que nos echan un cable para largarnos del planeta porque hemos sido capaces de acabar con las condiciones que nos permiten vivir en él. Ni tan siquiera que los cachondos nos elijan un sitio para vivir justo al lado de un puto agujero negro. Son pentadimensionales pero tienen poco ojo para elegir vivienda, con la de planetas que orbitan estrellas que hay en el universo. 

El verdadero problema, el problema de verdad, el problemón, es que una vez que hemos sido capaces de saltar de un sistema estelar a otro, de una galaxia a otra, tenemos que plantearnos la cuestión del mardito parné.

Cuando llegaron el economista ya estaba allí

No, no es un intento de hacer el cuento más corto y sórdido de la historia ni el de competir con el pobre dinosaurio. El caso es que aunque a día de hoy aún no sepamos si podremos dominar la tecnología para hacer viajes interestelares, los economistas ya se han puesto a estudiar cómo se tienen que adaptar cosas tales como el comercio, los impuestos, las acciones, seguros, políticas monetarias, etc., en esa situación. Por si acaso amigo, solo por si acaso.

Seguramente habrá leído o escuchado esa anécdota de un tal Faraday que estaba investigando sobre cosas electromagnéticas allá por el siglo XIX y el ministro de Hacienda de turno le preguntó para qué servía eso y nuestro protagonista le respondió: «Sir, no lo sé pero algún día podrá gravarlo con impuestos». Ahora la cosa ha cambiado, aún no sabemos si podremos viajar entre estrellas o galaxias pero sí sabemos cómo pagaremos impuestos en caso de que podamos hacer tales viajes. Para que luego digan que no somos previsores.

El problema al que se tienen que enfrentar los economistas y, sobre todo, los ministros de Economía y Hacienda es el de hacer los cálculos para poder cobrar impuestos en sus dominios aunque estos dominios impliquen más de un sistema estelar y esos sistemas estén alejados muchos años luz entre sí. El gran nudo gordiano que hay que cortar concierne a que el tiempo no es absoluto en el universo y pasa más o menos lento dependiendo del movimiento relativo entre observadores o de si estos observadores están sufriendo una gravedad mayor o menor. Esta tontería hace que definir precios, intereses o impuestos tenga que ser estudiado desde una perspectiva relativista, de relatividad especial o general, la relatividad de Einstein para entendernos.

Antes de entrar de lleno en el problema de la economía relativista quizás sea conveniente perder un poco el tiempo, por supuesto esto es relativo, en dar unas pinceladas sobre relatividad especial y general y sobre dilataciones y contracciones temporales.

En relatividad no todo es relativo

La relatividad dice muchas cosas pero de entre todas las cosas que dice no menciona ni una sola vez que todo sea relativo. Al contrario, lo que una buena teoría de la relatividad establece son los elementos que son invariantes, inamovibles, las vigas maestras de toda la construcción física. 

¿Qué se necesita para definir un principio de relatividad? Pues necesitamos dos ingredientes, a saber:

1. Necesitamos identificar los observadores que tienen que cumplir escrupulosamente con nuestros requerimientos (la teoría relativista en cuestión).

2. Necesitamos definir qué leyes de la física permanecerán inalteradas al cambiar entre uno u otro de entre los observadores elegidos en el punto anterior.

3. Necesitamos encontrar una cantidad absoluta, invariante, inalterable, inamovible, impertérrita, incólume, (creo que ya lo vais pillando), sobre la cual todo observador de los anteriores está de acuerdo.

Esto nos puede dar una pista para deducir que hay varios principios de relatividad o teorías relativistas. Y como muestra:

Relatividad de Galileo

Observadores – Observadores que se mueven en línea recta y a velocidad constante, la velocidad cero está permitida. A estos los llamamos observadores inerciales.

Leyes de la física invariantes – Las leyes de la mecánica (leyes de Newton) son las mismas para todo observador inercial. Si definimos una ley mecánica, por ejemplo F=ma, para un observador inercial y luego le pedimos a otro observador inercial que se mueve respecto al primero que defina dicha ley también nos dirá que es F=ma. Esa ley es invariante para todo observador inercial.

Cantidad absoluta – El tiempo transcurrido entre dos fenómenos cualesquiera. Sí, el tiempo para Galileo es absoluto, cualquier observador inercial dirá que ha pasado un tiempo T entre dos sucesos y cualquier otro estará de acuerdo con este tiempo T. 

Relatividad Especial de Einstein

Observadores – Los observadores inerciales igual que en el caso galileano.

Leyes de la física invariantes – Todas las leyes de la física, las de la mecánica, electromagnetismo, interacciones fuertes o débiles, las que sean. Cualquier observador inercial definirá las mismas leyes.

Cantidad absoluta – La velocidad de la luz en el vacío. Cualquier observador inercial, independientemente de su movimiento respecto a la fuente de emisión de la luz en el vacío, medirá la misma velocidad de la luz.

Aquí es donde empieza la diversión. Al contrario que en Galileo, para Einstein lo absoluto no es el tiempo transcurrido entre dos sucesos, lo absoluto es la velocidad de la luz en el vacío. Así pues, los tiempos y los espacios recorridos por algún sistema en un proceso físico serán percibidos como distintos por distintos observadores dependiendo de su velocidad relativa con dicho sistema. Así que, como veremos ahora en un momento, los tiempos y las distancias son relativas al observador y no absolutas.

Relatividad General de Einstein

Observadores – Cualquier observador independientemente de su trayectoria o estado de movimiento.

Leyes de la física invariantes – Todas las leyes de la física.

Cantidad Absoluta – Velocidad de la luz medida en cada punto del espacio-tiempo en el vacío. 

Aquí todo se descontrola, la relatividad general de Einstein es una teoría que nos dice que la gravedad no es más que el reflejo de la geometría cambiante del espacio-tiempo cuando interacciona con las densidades y flujos de energía de otros campos físicos como el electromagnético, el débil, etc. Llegamos a tal extremo que distinguir entre lo que es espacio y tiempo propiamente dicho no es que sea relativo al observador es que solo se puede hacer en casos muy determinados. En general, tal distinción no es posible hacerla en toda la extensión del espacio-tiempo. En puntos aislados y entornos pequeños de tales puntos siempre es posible distinguir entre espacio y tiempo pero tal distinción pierde sentido si intentamos extenderla a todo el espacio-tiempo.

Jugando con el tiempo

Vamos a dar dos pinceladas breves sobre la relatividad del tiempo según distintos observadores en distinto estado de movimiento o inmersos en regiones con distinta intensidad de la gravedad. Para ello vamos a hacer unos dibujitos. 

Imaginemos que nos consideramos los chismosos del espacio-tiempo y definimos un estado que consideraremos en reposo ya que, evidentemente, estamos en reposo respecto a nosotros mismos. Vamos a ver qué hacen otros observadores por ahí. 

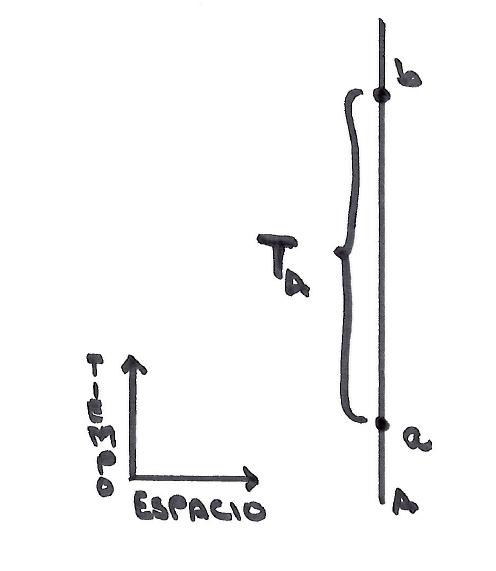
Si ahora vemos que Alicia (A) está en reposo respecto a nosotros podremos dibujar su evolución en el espacio-tiempo como sigue:

Alicia (A) lleva un reloj que entre los puntos a y b marca que ha pasado un tiempo TA. A está en reposo, por eso representamos su trayectoria en el espacio-tiempo por una línea vertical indicando que ocupa la misma posición para todo instante de tiempo. Este es uno de los diagramas espaciotemporales más simples posibles.

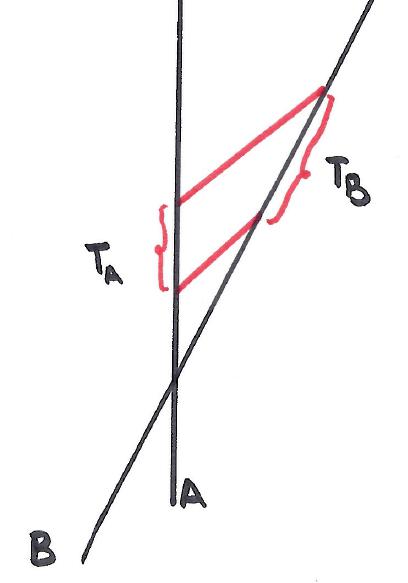
Consideremos que ahora tenemos además a Benito (B) que se mueve en línea recta y a velocidad constante alejándose de Alicia (A). El diagrama en esta ocasión sería:

A está en reposo y B se mueve respecto a ella a velociad constante y en línea recta. Si en dos instantes de tiempo A envía dos señales de luz (indicadas por las líneas rojas) a B resulta que el tiempo entre una señal y otra para A es TA y para B es TB. Como se ve en el dibujo, dado que la luz siempre se mueve a la misma velocidad para todos los observadores, se cumple esta condición:

Si, para A el tiempo en B pasa más despacio, dos señales que para ella han salido en un tiempo TA las ve que llegan en un tiempo mayor TB según el reloj de B. 

Esto es importante, el efecto es que desde A el tiempo en B pasa más despacio.

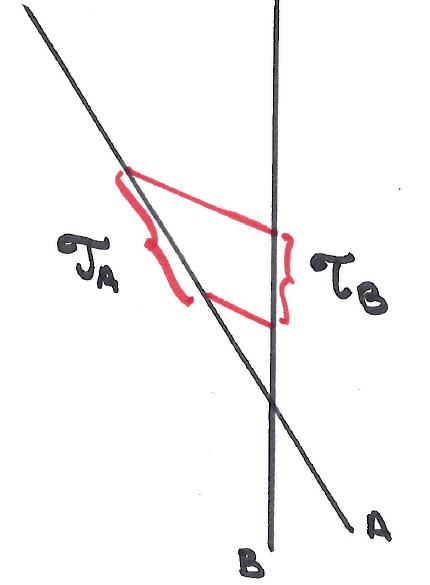
Pero claro, esto es relativo porque desde el punto de vista de B la cosa está en que A es la que se está alejando de él con velocidad constante y en línea recta. Es decir, para B la cosa es tal que así:

Si ahora es B quien envía un par de señales luminosas a A verá como el tiempo en el que las recibe A es mayor que el tiempo en el que él las ha emitido. Ocurre que para B se cumple:

Este es el verdadero significado de la relatividad. Para B es el reloj de A el que va más lento que el suyo.

¿Quién lleva razón? Los dos.

Siempre y cuando ninguno se de la vuelta y puedan comparar los relojes. En tal caso la simetría se rompería y uno de ellos efectivamente habría ido más lento que el otro. Esto es lo que se conoce como la paradoja de los gemelos. El folclore relativista sobre el tema versa tal que así:

Una pareja de gemelas es separada. Una de ellas se queda en la Tierra y la otra se mete en una nave espacial que tras un determinado tiempo da la vuelta y se dirige de nuevo al planeta. Al reencontrarse, las gemelas ven estupefactas como la que se ha quedado en la Tierra ha envejecido mucho más que su hermana astronauta.

Esto puede parecer un tanto sorprendente porque los efectos relativistas deberían de ser simétricos. Sin embargo, no hay ninguna paradoja, la razón de poder distinguir entre una gemela y otra es pura y simple geometría. Claro, geometría un tanto rara para nosotros que no tenemos experiencias relativistas, es geometría de Minkowski.

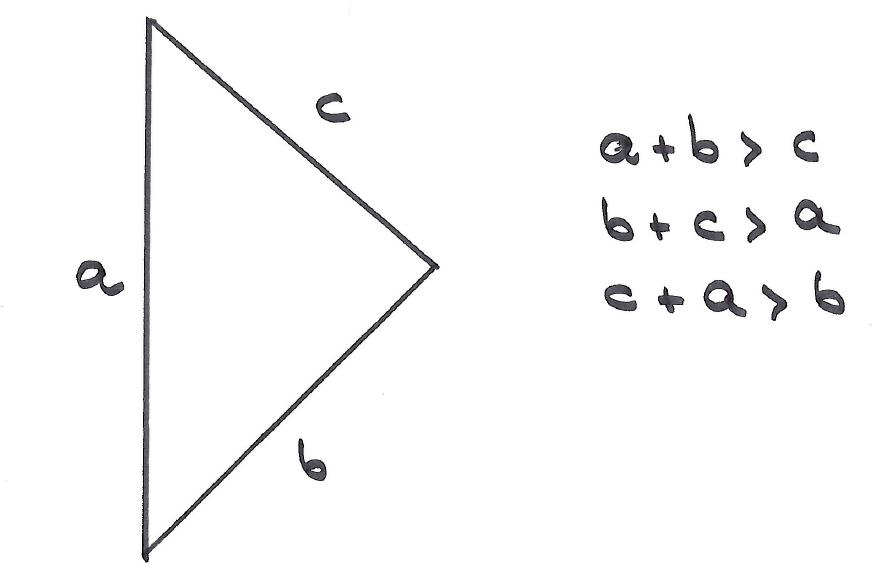
En nuestro mundo cartesiano todos estaremos de acuerdo en lo siguiente:

La longitud de cualquier lado de un triángulo es, «evidentemente», menor que la suma de los otros dos lados.

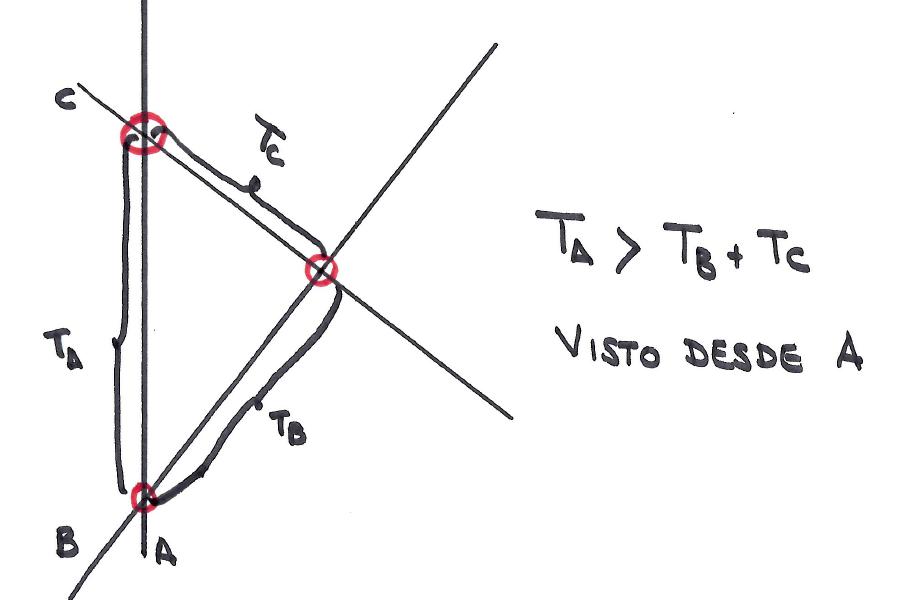
Hay que tener cuidado con lo «evidente» porque en el espacio-tiempo relativista ocurre justo lo contrario:

El tiempo medido entre dos sucesos, que las gemelas se separen y se reencuentren, siempre es mayor al medirlo desde un único sistema de referencia. En este caso una gemela se queda en el sistema A y mide los sucesos de separación y reencuentro desde dicho sistema. La otra gemela que se va y vuelve, en algún momento ha tenido que cambiar de sistema de referencia, así que mide el tiempo de separación y reencuentro desde dos sistemas de referencia. La relatividad nos dice que el tiempo será más largo para el observador que mide el tiempo transcurrido entre los dos sucesos desde un único sistema de referencia.

Esto es una de las maravillas de la relatividad, maravilla que comprobamos a diario en los GPS por ejemplo.

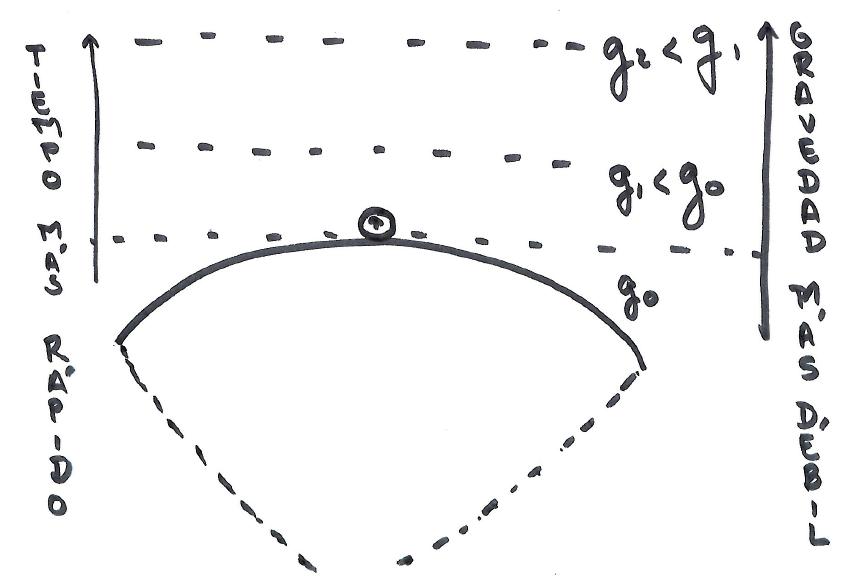
Hasta aquí solo hemos hablado de observadores en movimiento, pero qué pasa cuando hay gravedad de por medio. Pues lo que nos dice la teoría, refrendada por el experimento, es que cuanto mayor sea el campo gravitatorio en una zona más lento irá el tiempo en dicha zona.

El lío con la economía interestelar

Supongamos que por arte de birlibirloque, —entendedme, me moría de ganas de escribir esta palabra en Jot Down—, conseguimos movernos con relativa facilidad por el universo. Qué sé yo, hemos dominado la energía oscura y construimos burbujas WARP, construimos agujeros de gusano que se mantienen estables y abiertos, lo que se nos ocurra. Pues entonces querremos tener, allende las galaxias, nuestras cositas imprescindibles; nuestras bebidas energéticas, nuestras gafitas de pasta, nuestras camisas de cuadros o nuestras cintitas de Camela para cuando vayamos a dar un paseo intergaláctico y dominguero. Y entonces empezará el pifostio padre.

¿Cómo pagaremos los productos? ¿A qué valor? ¿Cómo se calculan los intereses? ¿Cómo aseguraremos transacciones y compras?

Pensemos por un instante en la situación de que uno de nosotros compra desde la Tierra un producto en un planeta, Wecan, que está a cien años luz. Supongamos que por los avances tecnológicos solo necesitamos diez años para ir de la Tierra a Wecan. Aun así cualquier transacción es difícil por las siguientes razones:

1. Si vamos desde la Tierra a Wecan empleando velocidades cercanas a la de la luz o metiéndonos por agujeros de gusano, etc., sufriremos dilataciones temporales. Para nosotros pasará mucho menos tiempo que para el comerciante de Wecan. 

2. Seguramente en Wecan con los años se genere inflación y los precios aumenten, esperemos que de forma acorde al aumento del poder adquisitivo de los wecanianos. Pero para nosotros ha pasado menos tiempo que para el señor de Wecan. ¿Quién fija el precio?

3. Hay una solución, fijar un precio de salida en el tiempo del que va a vender y meterle un interés que asegure que el vendedor no pierde dinero al hacer esta transacción. Dicho interés tendrá en cuenta la dilatación temporal del comprador en tránsito desde su planeta de origen hasta el de llegada. Los intereses los tienen que acordar entre los dos involucrados.

4. Pero es que si además el universo se está expandiendo aceleradamente, como es el caso, las distancias entre galaxias aumentan cada vez más y tanto más cuanto más alejadas estén inicialmente el par de galaxias en cuestión. En fin, que hacer un viaje intergaláctico desde una galaxia a otra en este contexto puede ser tan desastroso como que al llegar ya no esté ni una galaxia ni haya galaxia a la que volver. Así que el comercio entre galaxias muy alejadas sería poco recomendable. 

¿De qué va todo esto, amigo?

Parece una chorrada. Lo es. Lo es y no lo es. Aunque parezca mentira ya en 1978 se empezó a pensar sobre el comercio interestelar. De hecho, apareció un artículo sobre el tema que se publicó en 2010, pero escrito en el maravilloso año 1978, por un tal Paul Krugman, premio nobel de Economía entre otras cosas. Podemos decir que Krugman escribió este artículo en broma en respuesta a los artículos que existían sobre el comercio interplanetario y porque estaba hasta los cojones del poco futuro que le deparaba el mundo universitario de su tiempo. 

El artículo está aquí: 

«The Theory of Interstellar Trade». Publicado en Economic Inquiry 48 (2010). 

Sobre la influencia de los efectos de la relatividad especial en la economía hay dos artículos interesantes y divertidos: 

«Spacetime Finance» de Spen Haug para la revista Willmott. En este artículo encontraréis una amplia discusión sobre el valor que se le asigna a un determinado bien económico en un contexto relativista. 

«Tax in the Final Frontier: A Theory of Interstellar Tax» del profesor Adam Chodorow. En este artículo, escrito en clave de humor para la revista Tax Analysts, se habla sobre los efectos relativistas en el cálculo de los impuestos.

Y llegados a este punto podríamos pensar que todo esto es una chorrada porque nunca encontraremos situaciones, al menos en nuestra generación y las próximas venideras donde esto de la economía relativista tenga la más mínima importancia o utilidad. Si estáis pensando en ello estáis totalmente equivocados. 

En nuestro mundo, de hecho, podríamos definirlo como aquello que sustenta una red internáutica. Hoy día las transacciones comerciales, la bolsa especialmente, no están confinadas a una ciudad ni tan siquiera a un país. El comercio a día de hoy es global. Y eso implica que las transacciones, las operaciones de oferta de venta, las órdenes de compra, la información de las cotizaciones, etc., tienen que estar perfectamente sincronizadas y localizadas en el espacio. 

Para conseguir eso tenemos que hacer uso de las impresionantes redes de satélites de posicionamiento, los GPS, y de los de transmisión de datos que hemos sido capaces de diseñar y de poner en funcionamiento. Es de fundamental importancia que los datos sean transmitidos, recibidos y procesados de forma simultánea debido a que cualquier desincronización podría dar ventaja a unos participantes sobre otros. Tenemos que pensar que los satélites están en órbita y se están moviendo respecto a nosotros que estamos en la superficie terrestre, por lo que están sometidos a procesos de dilatación temporal de la relatividad especial. Pero no podemos olvidar que tenemos otro efecto, los satélites están sometidos a menor gravedad que la superficie por lo que su tiempo pasa más rápido. Ambos efectos, el especial y el general-gravitatorio, son opuestos y el que gana es el gravitatorio. Todo eso se tiene que tener en cuenta para que el mercado no sufra consecuencias indeseables, sobre todo para algunos, de una mala sincronización de sistemas.

Todo esto ha sido estudiado en este artículo: «Relativistic Statistical Arbitrage» de los autores A. D. Wissner-Gross y C. E. Freer en 2010 en la revista Physical Review E 82. 

Así que tomen estas casi tres mil palabras como una perfecta excusa para hablar de relatividad y para considerar que aún nos quedan muchos problemas a los que enfrentarnos conforme vayamos avanzando en nuestro paseo por el universo.

Nos seguimos leyendo…